

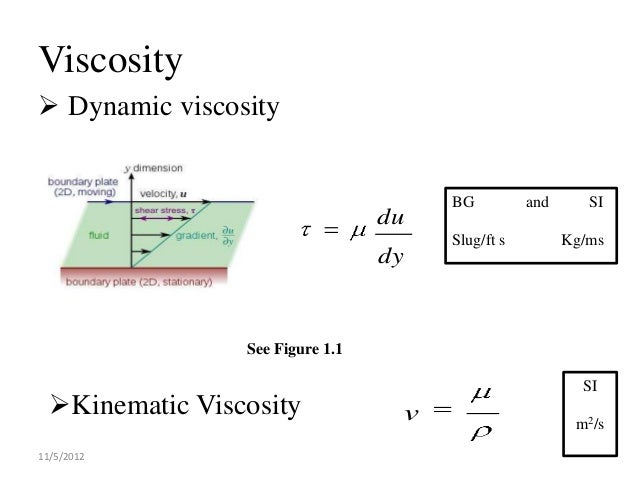
In the above equation, µ is referred to as the dynamic viscosity and is defined for different fluids as a factor of the kinetic viscosity. Where 𝛾 is the shear strain and d𝛾/dt is the strain rate. In this case, viscosity is defined by the relationship between stress and strain, as shown in equation 3. In order for a fluid to resist shear stress, it must be in motion.
These fluids, which include gasoline, alcohol, mineral oil, and water, are known as Netwonian fluids. It is also true that there are fluids where the viscosity remains constant irrespective of the shear force for constant temperature. The Relationship Between Stress and Strainįrom equation 2, we see that if the shear rate is constant, then the shear stress is zero, even under changing viscosity. For fluids, this is called fluid flow, which does not occur without resistance. Similar to Newton’s laws for classical motion, when a force is applied to a fluid, the result is motion. The greatest source of stress is the fluid viscosity. For the most accurate calculation, the elements should be infinitesimal. The shear stress of a fluid can be defined as a unit area amount of force acting on the fluid parallel to a very small element of the surface.

From equations 1 and 2, a definition for the shear stress in fluids follows: In the figure above, the relationship between shear stress and the shear rate is illustrated. Relationship between shear stress and shear rate Where µ is the viscosity and dµ/dy is the shear rate. The above equation gives the average shear stress per unit area. Where 𝞽 is the shear stress, F is the applied force, and A is the cross-sectional area parallel to the direction of the applied force. What Is Shear Stress?Īs the name implies, shear stress refers to the action of a force applied to a material, as indicated by equation 1. An understanding of this phenomenon is important for designing, monitoring, and controlling systems, which typically include electronics and PCBAs, for a wide range of applications and fields, including aerospace, automotive, energy, and industrial processing. In fact, there is a Newtonian law that defines the shear stress in fluids.ĭepending upon the medium, shear stress may cause a change in fluid flow between layers. Specifically, Newton helped us understand viscosity, which describes the thickness of a fluid and affects its resistance to flow due to internal forces. It may come as a surprise, however, that Newton was also instrumental in our understanding of fluid flow. Collectively, these are important, as they are foundations for our understanding of classical physics. Sir Isaac Newton is quite famous for developing the three laws of motion. As shown this can be interpreted as a rotation of the line connecting A-B.What is the relationship between dynamic and kinematic viscosities? The introduction of viscous forces requires a model to obtain a set of conditions on the flow field to express the viscous stress tensor, direction. We end with the introduction to similarity solutions to the Navier-Stokes equations through an example problem. We will then show how this seemingly formidable set of equations can be simplified for a number of rather practical flow problems resulting in exact, analytical solutions. We will simplify the equations for incompressible constant property flows, which are useful for a vast majority of flow situations. In this section we develop the governing equations for viscous flows resulting in the Navier-Stokes equations.


 0 kommentar(er)
0 kommentar(er)
